Основоположник теории хаоса получил Абелевскую премию

Норвежская академия наук и литературы отдала Абелевскую премию 2014 года советскому физику и математику Якову Синаю из Принстонского университета в Нью-Джерси. Награда вручена за «фундаментальный вклад в динамические системы, эргодическую теорию и математическую физику».

Джордан Элленберг (Jordan Ellenberg), математик из Университета Висконсина в Мэдисоне, вручавший награду, сказал, что Синай работал над вопросами, касающимися реальных физических систем, «с душой математика». Он разработал инструменты, которые показали, как системы, выглядящие внешне разными, могут иметь глубокие сходства. Так же как Исаак Ньютон когда-то доказал, что падением яблока и движением планет руководят одни силы.

Яков Синайматематик, Принстонский университет

Математика и физика должны идти вместе, как лошадь и повозка.

Синай, которому сейчас 78 лет, знаменит за свою работу в области сложных динамических систем, включающюю так называемую теорию хаоса. Ее можно рассматривать как применение идеальных механических законов к беспорядочным сложностям реального мира. Законы движения Исаака Ньютона дают приблизительное описание того, как движутся объекты под влиянием сил в некоторых простых случаях (движение планет, например), принципы, регулирующие реальное динамическое поведение, как правило, куда сложнее. Это относится к предсказыванию погоды и атмосферных явлений, динамике народонаселения, физиологическим процессам (например, сердцебиению) и многому другому.

Предсказывая непредсказуемое

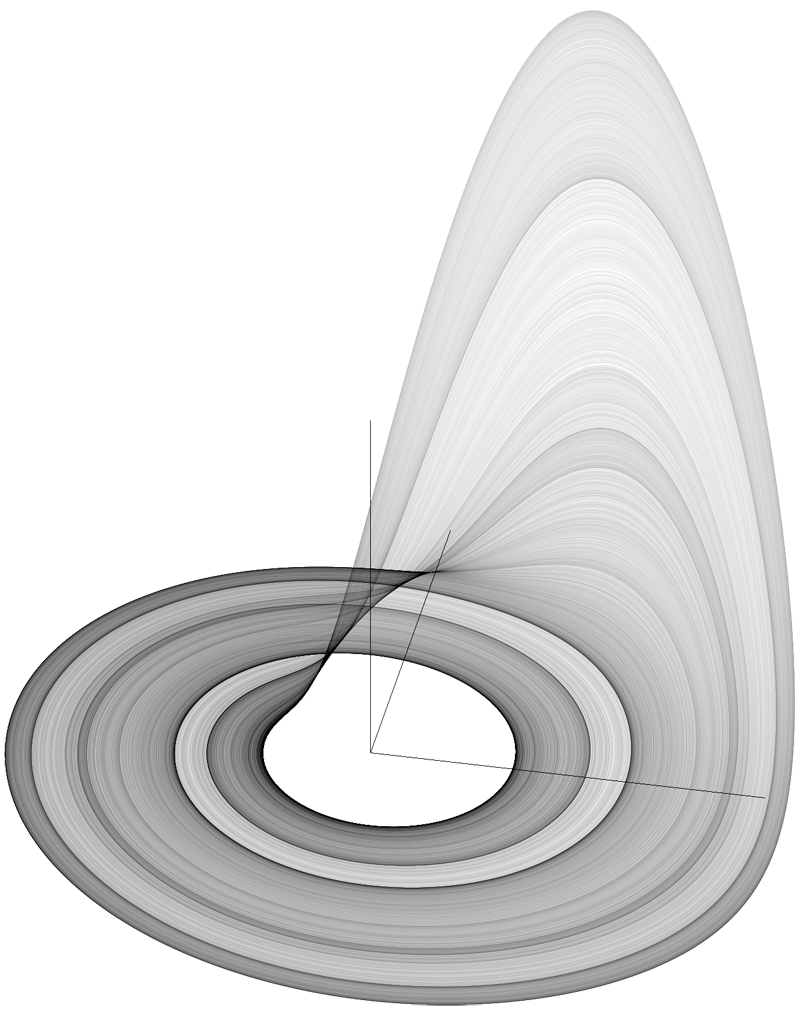Иногда эти движения имеют случайный характер, например, покачивание мелких частиц тепловым шумом. Это стохастические динамические процессы. Чтобы подорвать идеальную предсказуемость законов Ньютона, достаточно присутствия слишком большого количества взаимодействующих тел, как в случае потока жидкости. Даже с тремя объектами, следующими ньютоновским законам, крайне малые различия в начальных условиях могут привести к абсолютно непредсказуемым результатам в долгосрочной перспективе, таким образом и возникает случайность даже в абсолютно предсказуемых процессах.

Этот вид «детерминированного хаоса», как теперь известно, присутствует в орбитах планет Солнечной системы. Синай разработал математические аппараты для изучения подобного поведения и определил параметры, остающиеся неизменными, даже если траектории объектов в сложных динамических системах становятся непредсказуемыми.

Интерес к этим вопросам появился уже в конце 1950 годов, когда он был студентом Андрея Колмогорова, одного из величайших физиков-математиков XX века и одного из основателей теории вероятности, в Московском государственном университете. Синай и Колмогоров продемонстрировали, что даже для динамических систем, чье детальное поведение непредсказуемо (из-за детерминированного хаоса или случайности), существуют параметры, измеряющие степень «сложности» или непредсказуемости движения. 

Системы, чья энтропия К-С равна нулю, можно точно предсказать; системы с ненулевой энтропией К-С полностью предсказать нельзя, они включают в себя хаотическую систему.

Параметр сложности

Параметры, такие как энтропия К-С, связаны с тем, как тщательно система исследует все состояния, которые она может принять. Грубая система, которая определяет все эти состояния, называется эргодической. Одной из наиболее важных модельных систем для изучения эргодического поведения является бильярд Синая, который он ввел в 1960х годах.

В этой идеализированной системе частица отскакивает без потери энергии по квадратному периметру, в центре которого круглая «стена». Эта динамическая система первая доказала, что траектории всех частиц эргодичны, они проходят через все доступное пространство. Они также хаотичны, в том смысле, что малейшие различия в начальной траектории движения частиц довольно быстро приводят к абсолютно разным движениям.

Своей работой Синай заложил основу для понимания турбулентного потока жидкости, микроскопической статистической теории газов и хаоса в квантово-механических системах. Премия Абеля, названная в честь норвежского математика Нильса Хенрика Абеля (Niels Henrik Abel) (1802-1829 гг.), не менее престижна, чем Нобелевская премия, церемония награждения проходит каждый год с 2003 года. Размер премии составляет 6 млн норвежских крон или около $1 млн. 

Майкл Берри (Michael Berry)физик и математик, Университет Бристоля, Великобритания (он работал над хаотическим квантовым бильярдом и другими аспектами сложной динамики)

Я очень рад, что Синай, чьей научной и общественной работе я симпатизирую, получил этот приз.

Элленберг говорит, что работа Синая продемонстрировала, что в математике «хорошее определение так же важно, как и хорошая теорема». В то время как физики имели лишь примерное представление о том, что такое энтропия, говорит он, Синай спросил: «О чем конкретно вы говорите?», заставив дать точное определение, отправную точку любой современной математической теории. Это помогло Синаю определить наиболее важные и принципиальные аспекты в поведении системы.